II.3 Measuring Social Network Structure
Other people are the greatest source of pleasure, and the main cause of misery. Only by connecting with others in meaningful ways in social networks are we sentient productive creatures. Skillfully navigating social networks is the key ingredient for success and happiness. “Social Network Analysis” or SNA is the science that makes “networking” measurable. SNA tracks relations between different people through the structure of their network. SNA applies graph theory to determine the strength of interactions between individuals. The more somebody connects groups of otherwise unconnected people, the more social capital this person has. The strength of these interactions between people has been traditionally measured through surveys, asking an individual questions such as “name all people to whom you went for advice last month” to generate a list of this individual’s interactions in the last month. However, this way of data collection is prone to bias, as people might not remember whom they asked. Human memories are short, and skewed towards the most recent past. Therefore, using archives of electronic communication offers a more robust way of collecting these interaction records between individuals. Our team at MIT has been at the forefront of using e-mail and other communication archives to analyze social networks for the last twenty years.
Social network analysis applies graph theory, and measures communication in the network by analyzing the structure of the network. Key network metrics are degree centrality, and betweenness centrality. Degree centrality of a person is the number of direct contacts a person has, for example by exchanging e-mail with others. Betweenness centrality of a person measure how much information flows through the person, in other words, how much the person is on all shortest paths through the network. The more somebody is a gatekeeper connecting disparate communities, the higher her betweenness centrality.
Figure 21. Difference between betweenness and degree centrality in a network
Figure 21 illustrates the difference between degree centrality and betweenness centrality. It shows an e-mail communication network of 39 students in my course working in seven teams, collaborating on seven different projects. Each network node is a student, each connecting line is at least an e-mail exchanged between the two students. The shorter the connecting line and the closer to students are together, the more e-mails the two students have exchanged. In the network visualization at right, the nodes representing the students are sized by degree centrality, in the picture at left by betweenness centrality. We see that Mary and Max have the highest degree centrality, each exchanging e-mails with seven other students. However, Mary’s betweenness centrality is much higher than Max’, as she is the gatekeeper of the network, connecting all the other teams, while Max is central only for his own team, with links to just two students outside his team. Compare this to Beth, who also only connects with one person outside of her team, Joe. Her degree centrality is five, as she connects to her four teammates, plus Joe. Beth’s betweenness is higher than Max’s however, as she is the exclusive gatekeeper for her team members to the other teams through Joe while in Max’s team there are two other connectors to the other teams.
A second useful metric is contribution index, which measures how active as a sender of e-mails and other messages somebody is. Figure 22 illustrates the contribution index of the same group of 39 students as mentioned in Figure 21.
Figure 22. Contribution Index example
In Figure 22 the x-axis shows the numbers of messages a student exchanged, i.e. sent and received, while the y-axis shows the contribution index of the student, which is defined as +1 if the student only sends e-mails without receiving any, and -1 if the student only receives e-mails without sending any. If the contribution index of a student is 0, she has perfectly balanced communication behavior, with sending and receiving the same number of messages. In the example in Figure 22, John exchanges the most e-mails, close to 80, he shows a passive e-mailing behavior, with a negative contribution index of -0.6. Rose on the other hand exchanges less e-mails, slightly less than 20, however she shows proactive behavior, with a contribution index of about 0.5 sending much more e-mails than she receives.
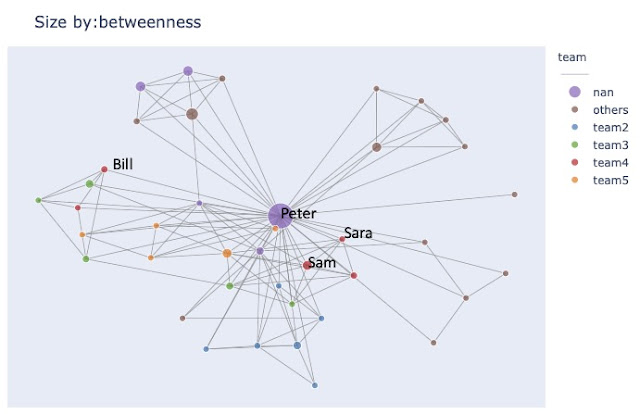
Figure 23. Same course network including instructor, illustrating density and clustering of network
Figure 23 shows the same network as Figure 21, but with the teacher (myself) added. Note how the density of the network increases, as I am connected to almost all the students directly. This also means that as the hub in the network, I am connecting a lot of otherwise unconnected people. This is called “closing the transitive triad”, meaning that if I have links to two people, for example Sam and Sara, I can introduce them to each other to connect them, thus completing the triangle or triad. The more triads there are in a network, and the higher the density of the network, the more cohesive is the community.
The length of the link from me to Sara is proportional to the number of e-mails Sara and I have exchanged, the shorter the link, the more e-mails we have exchanged. The more e-mails we exchange, the “stronger” is the tie. As the link from me to Bill is much longer, the tie between Bill and I is called a “weak tie”. In social network theory, strong ties represent social capital and trust, while weak ties are useful for information exchange.
Another metric that measures cohesion is the degrees of separation between any two people in the network. For instance, the degree of separation between Bill and Sara is two, meaning that it takes two hops in the network for Sara to reach Bill. This is also called the path length from Sara to Bill, the shorter the average path length in a network is for any two people to reach each other, the more connected and cohesive the community is. A network with short average path length will also be more suited for spreading new ideas quickly, as new ideas will quickly flow to all network members.



Comments
Post a Comment